Cominciamo a sporcarci le mani con esempi concreti e codici sorgenti introducendo la regressione lineare. Si tratta di un metodo di stima del valore atteso di una variabile dipendente Y, partendo dai valori di altre variabili indipendenti X1, X2, …, Xk.
Partiamo con un esempio semplice dove di variabili indipendenti ne abbiamo solo una: prendiamo in esame un ipotetico dataset che elenca le superfici di alcune abitazioni e i relativi valori di mercato. Utilizzando la regressione lineare potremo avere una stima del prezzo di vendita di un’abitazione la cui superficie non rientra tra quelle in elenco.
In strumenti come Excel è semplice creare una regressione lineare: si crea un grafico a dispersione xy dei valori in tabella e poi si aggiunge una linea di tendenza di tipo lineare. La nostra regressione sarà questa linea.
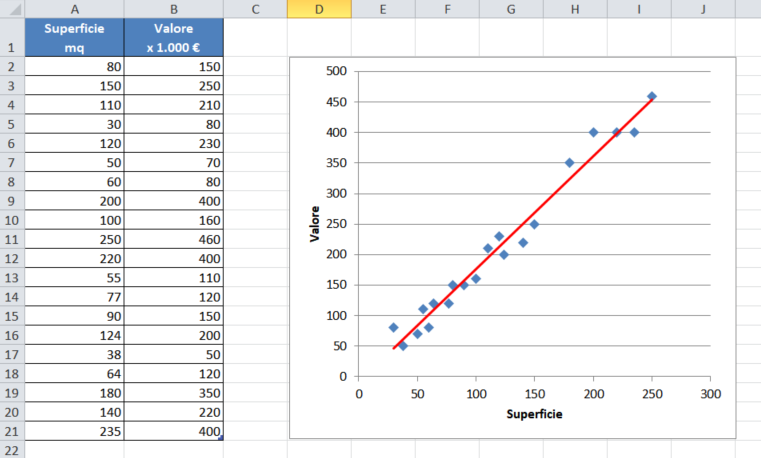
Una volta individuata la retta della regressione, le stime dei valori saranno sulla retta stessa.
Excel ci dice ad esempio che una abitazione di 167mq (superficie che non è in elenco) avrà un valore che non si discosterà troppo da 300.000€.
La regressione lineare rappresenta quindi quella retta del piano che minimizza la somma delle distanze tra lei e i punti del dataset. Ogni altra retta potrà diminuire la distanza di alcuni punti ed aumentare la distanza di alcuni altri, ma nel complesso la sommatoria di tutte le distanze della retta dai singoli punti aumenterà.
Ora, tra le infinite rette, come possiamo scegliere quella giusta?
Rispolveriamo i libri di geometria e andiamo a vedere come è definita la equazione di una retta in forma esplicita.
y = mx + q
dove y è detta variabile dipendente, m è il coefficiente angolare, x è la variabile indipendente, q è detta intercetta.
Analizzando i vari termini e coefficienti di questa equazione, possiamo dire che:
- x è un valore sull’asse orizzontale (in questo caso la superficie). Rappresenta quindi un dato in ingresso.
- y è un valore sull’asse verticale (in questo caso i valori stimati della abitazioni in base alla superficie). Rappresenta quindi un dato in uscita.
- variando q la retta si alza o abbassa lungo l’asse verticale, mantenendo intatta la propria l’inclinazione. Rappresenta quindi uno scostamento o bias.
- variando m la retta modifica la propria inclinazione (per m maggiori, l’inclinazione aumenta, per m minori, l’inclinazione diminuisce). Rappresenta quindi un coefficiente o peso applicato ai valori in ingresso
Possiamo quindi riscrivere l’equazione in termini più comuni al tema dell’intelligenza artificiale.
y = wx + b
con w (da weight, peso) che prende il posto di m e b (da bias) che prende il posto di q.
Modificando w e b possiamo ottenere tutte le infinite rette che è possibile tracciare sul piano cartesiano del grafico dell’esempio.
Abbiamo detto che tra queste, ne esiste solo e soltanto una che minimizza la propria distanza da tutti i punti del grafico.
Per trovarla ci viene in aiuto la funzione di costo (loss function), che ci fornisce una misura della distanza tra il nostro modello e quello ideale. Ne esistono di diversi tipi, a seconda della natura dei dati e del modello. Per la regressione si utilizza spesso la somma dei quadrati residui (o RSS da residual sum of squares).
Questa è definita come la somma degli errori al quadrato per ogni punto del nostro dataset. Per errore si intende la differenza tra il valore della y che leggiamo dalla tabella dei dati di esempio e il corrispettivo valore calcolato tramite l’equazione della retta usando i valori x della tabella degli esempi.

Ora, dopo esserci ripresi dalla visione di questa equazione, riflettiamo su cosa rappresenta la funzione di costo: dà una misura della distanza del nostro modello dalla soluzione ottimale. Quindi minore è il valore della funzione di costo, più il nostro modello si avvicinerà alla soluzione ottimale. Visto che stiamo sommando dei valori al quadrato, la funzione di costo non potrà mai essere negativa, quindi il valore più piccolo a cui potremo tendere sarà 0.
Assegnando i valori delle x e delle y (che abbiamo nella nostra tabella) e sviluppando la sommatoria, si ottiene una equazione dove le incognite sono il bias e il peso. Risolvendo questa equazione, otterremo quindi il valore di b e di w della retta di regressione.
Ok, qui stiamo parlando di regressione lineare in quanto stiamo cercando una retta su un piano. Più avanti vedremo regressioni più complesse, ma a meno di non ricordare molto bene il corso di Analisi Matematica dell’università, anche risolvere questa equazione può risultare un po’ ostico. Ci torna utile uno dei più importanti algoritmi del machine learning, che si presta bene alla ricerca di minimi (o massimi, se serve) in generale.
Il gradient descent
Si tratta di un algoritmo di ottimizzazione che consente di trovare i punti di massimo o di minimo di una funzione in modo iterativo. Come abbiamo detto al capitolo precedente, il nostro scopo è quello di minimizzare il valore della funzione di costo, per cui l’algoritmo del gradient descent si presta molto bene a questo scopo. Considerando che qualsiasi libreria o strumento che si occupa di intelligenza artificiale, ha una implementazione ottimizzata di questo algoritmo, non è necessario riscriverlo da zero. Noi lo andremo ad analizzare un po’ più nel dettaglio solo per capire come funziona.
Ipotizziamo che la nostra funzione di costo abbia un grafico di questo genere:
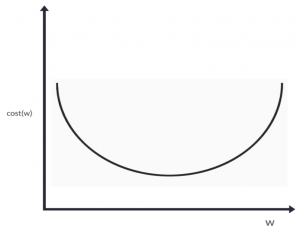
Il punto di minimo (sull’asse verticale) sarà nel punto inferiore della concavità, ed una volta trovato quello avremo anche trovato il valore di w con il quale si raggiunge. Partiamo con un valore a caso di w e calcoliamo la relativa funzione di costo. La situazione sarà simile a quella in figura dove il pallino rosso rappresenta il punto casuale appena calcolato e la bandierina verde rappresenta il minimo da raggiungere.
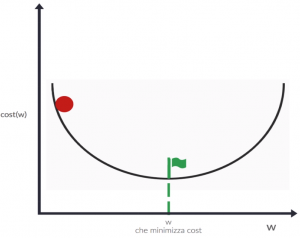
Per analogia con il mondo reale, cercare il punto di minimo è come lasciare cadere il pallino rosso in modo che possa seguire la curva e arrivi alla bandiera verde o nelle sue vicinanze (se di meglio non si riesce a fare…). Portiamo questo ragionamento a livello geometrico: calcoliamo la derivata della funzione costo nella posizione attuale del pallino rosso, ottenendo così un valore che ci dice come si evolve la curva al variare di w. Ad esempio, in questo caso la derivata sarà negativa, che significa che all’aumentare di w, si ha una diminuzione del valore della funzione di costo. Graficamente le informazioni fornite dalla derivata sono rese dalla freccia che vedete nella prossima immagine. Le due lineette verdi intorno alla bandierina rappresentano il nostro obiettivo minimo: dobbiamo arrivare almeno in quella zona per avere un valore soddisfacente.
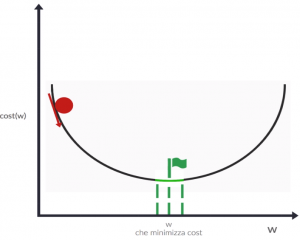
Ora, per spostare il pallino verso la bandierina dovremo variare w di una quantità di segno contrario a quello della derivata:
- Se la derivata è negativa (come nell’esempio in figura con il pallino a sinistra dove la curva scende se w aumenta), sarà necessario aumentare w.
Il prossimo valore della funzione costo sarà quindi minore del precedente perchè ci sposteremo a destra, verso il fondo - Se la derivata è positiva (ad esempio quando il pallino rosso è sulla parte destra della curva che sale se w aumenta), sarà necessario diminuire w.
Il prossimo valore della funzione costo continuerà ad essere minore del precedente, perchè ci sposteremo verso sinistra, ancora verso il fondo
Ma che valore utilizziamo? Già che abbiamo calcolato il valore della derivata, utilizziamo direttamente questo valore per variare w.
In verità applicheremo un coefficiente al valore della derivata chiamato learning rate, che serve ad evitare variazioni di w troppo bruschi che potrebbero portare il pallino ad oscillare troppo o addirittura divergere.
La funzione finale di aggiornamento sarà quindi (notare che il valore viene sottratto):
w' = w - lr * dw
dove:
- w è il valore attuale del peso
- dw indica il valore della derivata della funzione costo calcolata nel punto w
- lr è il learning rate da applicare
- w’ è il valore che peso assumerà dopo questa iterazione
Seguendo questo algoritmo, la nostra regressione lineare progredirà in modo analogo alla prossima immagine, dove a sinistra è riportata la funzione costo con il nostro pallino che scende (notare la retta tratteggiata della derivata, tangente alla curva nel punto in cui è poggiato il pallino) e a destra la retta di regressione con i dati del training set che si evolve man mano che la funzione costo si avvicina al minimo.
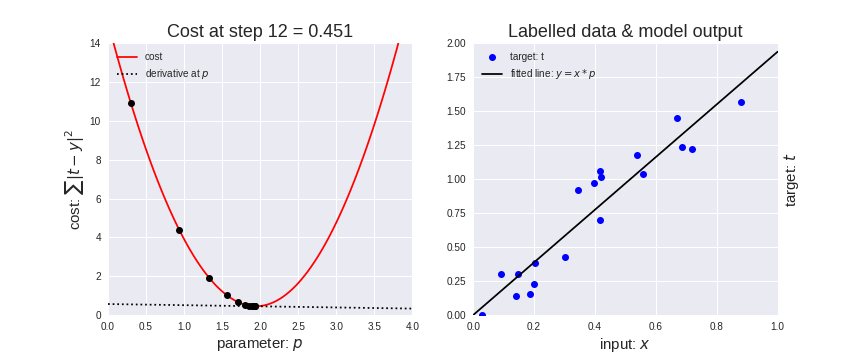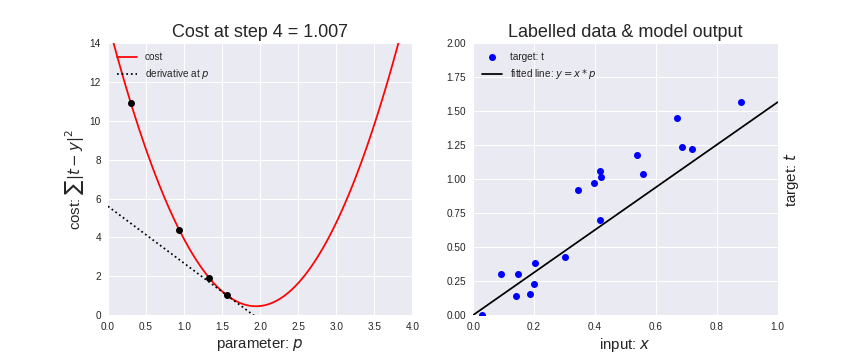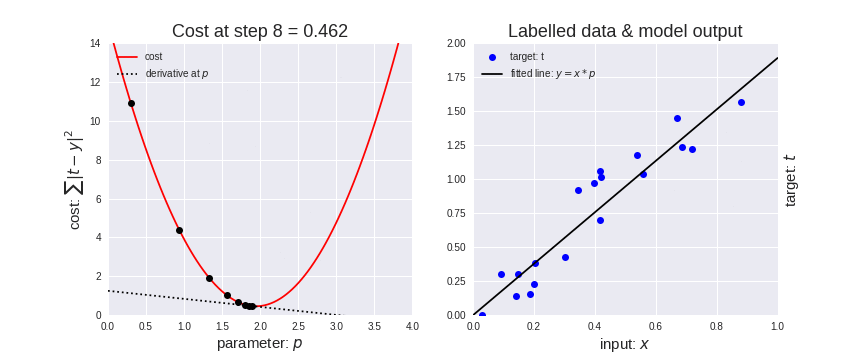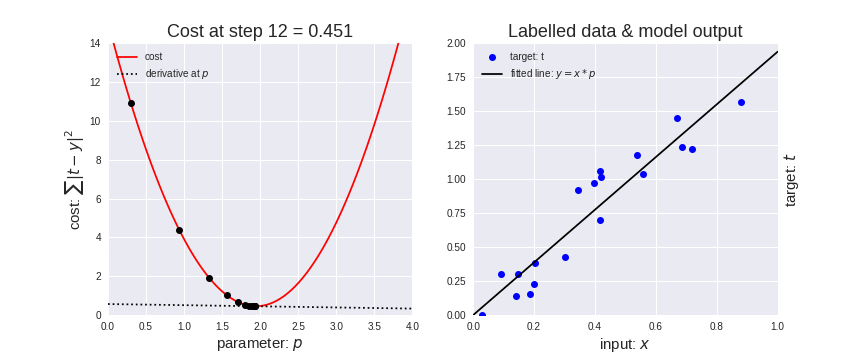
Come abbiamo detto, il learning rate modifica la velocità con cui il pallino rosso si sposta. Nell’immagine seguente si vede che se il learning rate è troppo piccolo, il pallino impiegherà molto tempo ad arrivare al minimo (animazione di sinistra). Se viceversa è troppo alto, il pallino tenderà a rimbalzare da una parte all’altra e addirittura tenderà ad allontanarsi (animazione di destra). Quindi scegliere il giusto learning rate (che è un iperparametro del nostro modello) consentirà di arrivare velocemente e senza troppi intoppi alla soluzione ottimale. Valori tipici sono compresi tra 0.0001 ed 1.
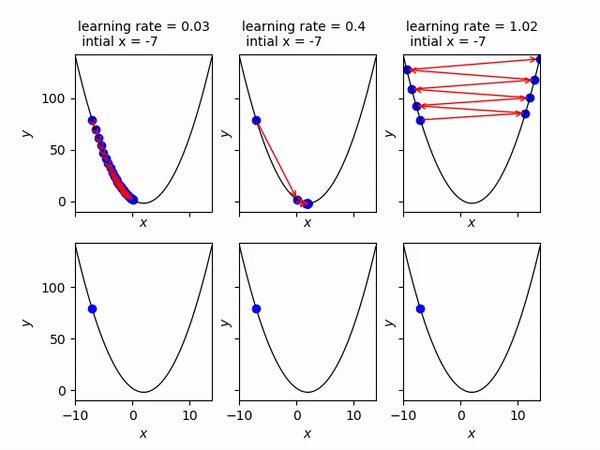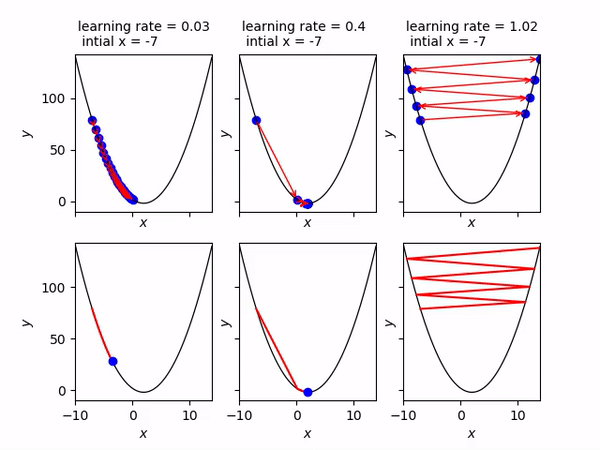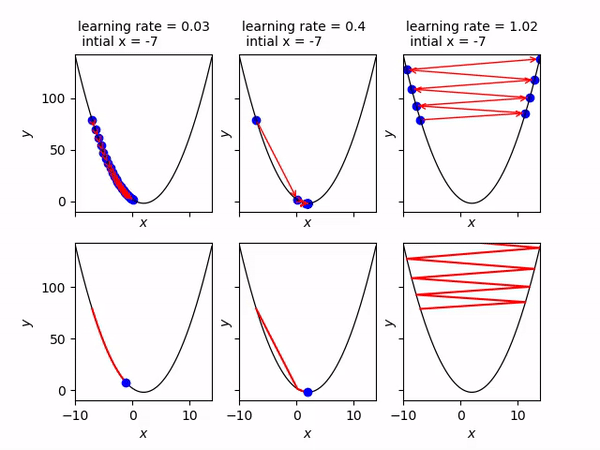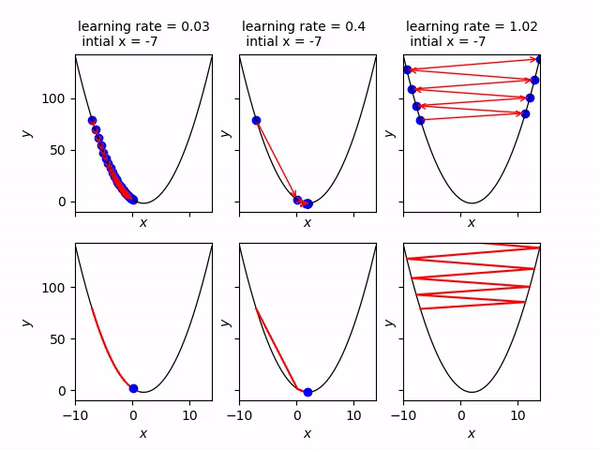
Ok, ma allora perchè questo metodo si chiama gradient descent ? Nel nostro caso abbiamo un’unica variabile indipendente x e quindi un unico peso w per il quale calcolare la derivata.
Se avessimo più caratteristiche per valutare il valore dell’abitazione (ad esempio superficie, distanza dal centro città, distanza dalla metropolitana, numero di piani, eccetera) allora invece di avere una curva su un piano avremmo una superficie curva in uno spazio multidimensionale.
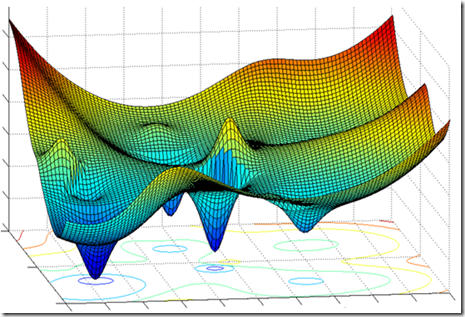
Per capire come spostare il nostro pallino su una superficie del genere dovremmo calcolare le derivate parziali per i pesi di ogni dimensione (superficie, distanza dal centro città, eccetera) in modo da poter capire come si evolve la superficie spostandosi lungo i vari assi. Tutte queste derivate parziali possono essere viste come le componenti di un vettore caratteristico chiamato gradiente. In sostanza, quindi, anche nel nostro esempio stiamo usando una versione particolare di gradiente.
Codice Python, at last…
Finalmente iniziamo a mettere le mani in pasta! Ovviamente, non andremo a reinventare l’acqua calda… Abbiamo visto velocemente che teoria c’è sotto il gradient descent e come viene utilizzato per il calcolo della regressione, ma non andremo a implementare l’intero algoritmo. Il motivo è che qualsiasi libreria che tratta gli strumenti di intelligenza artificiale implementa già tutte le funzioni che servono. Quindi vedremo come sfruttare per i nostri scopi quello che già c’è e che funziona egregiamente!
NOTA: il codice sorgente di questo esempio lo potete trovare qui
Iniziamo ad importare un po’ di librerie. In particolare:
- Pandas che mette a disposizione diverse utili funzionalità per la gestione dei dati (lettura, scrittura, manipolazione di dataset)
- SciKitLearn che è una delle più famose librerie di strumenti di intelligenza artificiale per Python (in questo caso importo solo quello che poi utilizzerò)
- MapPlotLib che è una libreria utilissima per disegnare grafici di qualunque tipo
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as pl
Importiamo il dataset direttamente dalla URL dell’Università della California. Si tratta di un dataset simile a quello del nostro esempio, con diverse proprietà delle abitazioni ed il relativo valore. Al momento ci interessiamo in particolare della proprietà che indica il numero medio di stanze delle abitazioni ed il relativo valore di mercato medio. Non è esattamente l’esempio nostro (noi avevamo ragionato sulla superficie), ma il ragionamento applicato sarà il medesimo.
# importiamo il dataset direttamente dalla URL dove è archiviato
dataset = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data",
# indichiamo che il file utilizza un numero indefinito di spazi come separatore di colonna
sep="\s+",
# indichiamo di utilizzare solo le colonne 5 e 13 che corrispondono al numero di stanze e al valore medio
usecols=[5, 13],
# assegniamo i nomi alle colonne
names=["STANZE", "VALORE"])
# diamo un'occhiata al dataset (solo le prime righe)
print("Diamo uno sguardo al dataset...")
print(dataset.head())
Ecco il risultato di questo pezzo di codice:
Diamo uno sguardo al dataset...
STANZE VALORE
0 6.575 24.0
1 6.421 21.6
2 7.185 34.7
3 6.998 33.4
4 7.147 36.2
A questo punto dividiamo il dataset in due sottoinsiemi: quello delle X (dati in ingresso, che corrisponde al numero di stanze in questo caso) e quello delle Y (dati in uscita, il nostro valore dell’abitazione). Ah! Noterete che in questo caso uso le lettere maiuscole. Il motivo è semplice: in questo caso X ed Y sono array di valori e non singoli valori.
# associamo ad X i valori di input
# NOTA: in questo caso l'unica proprietà è STANZE, ma in futuro potrebbero esserci diverse proprietà in input
# per cui con questa notazione stiamo dicendo a Pandas di escludere dal dataset la colonna VALORE e di fornire tutte le altre
X = dataset.drop("VALORE", axis=1).values
# associamo ad Y i valori di output
Y = dataset["VALORE"].values
In questo modo abbiamo creato degli array X ed Y, uno per ogni colonna del dataset iniziale.
Nota: se oltre al numero di stanze avessimo altre proprietà, X sarebbe una matrice e non un vettore. Ecco perchè per crearlo chiediamo a Pandas di prendere il dataset originale e semplicemente rimuovere la colonna valore: questo è un codice sorgente che sarà riutilizzabile in ogni caso. Lo vedremo nei prossimi articoli.
Ora dobbiamo preparare un set di training ed un set di test, partendo dai due array X ed Y.
Potremmo farlo ciclando su ogni elemento degli array, associandone un certo numero al training set, ed il rimanente al test set.
Ma in questo caso ci viene in aiuto SciKitLearn: visto che questa è un’operazione che viene fatta sempre, hanno deciso di implementare una funzione che fa già tutto il lavoro, in modo veloce e ottimale. Tra l’altro questa funzione si occupa anche di mescolare i dati (se serve) in modo da avere sempre dataset diversi.
# suddividiamo il dataset in due dataset, uno di training ed uno di test
# sfruttiamo una funzione di SciKitLearn che consente di fare questa operazione con un'unica istruzione
# il parametro test_size indica il rapporto tra la dimensione del set di test e l'intero dataset iniziale
# in questo caso il test_set sarà il 30% del dataset iniziale, ne consegue che il training set sarà il rimanente 70%
# di default l'istruzione mischia i dati del dataset in modo da ottenere sempre training e test set diversi
# è possibile modificare questa modalità tramite l'uso dei parametri shuffle e random_state
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3)
Bene, ora abbiamo un dataset di training ed uno di test con il quale valutare come si comporta il modello di regressione.
Non ci resta che eseguire la regressione. Anche in questo caso, la libreria mette a disposizione già la classe che fa per noi: LinearRegression. Sarà sufficiente istanziarla ed addestrarla e avremo il nostro modello già bello che pronto.
# istanziamo la classe di calcolo della regressione lineare di SciKitLearn
lRegr = LinearRegression()
# addestriamo la regressione passandogli i dataset di training
lRegr.fit(X_train, Y_train)
Valutiamo la bontà del modello. Gli forniamo in ingresso i dati del test set, ottenendo un array di valori predetti.
Questi valori predetti li confronteremo con i valori di output che ci aspettiamo (Y_test) usando due metriche diverse:
- una funzione costo: usiamo un errore quadratico medio che è simile alla funzione costo che abbiamo visto in precedenza, ma un po’ più robusto
- una funzione punteggio: è una funzione che rappresenta una proporzione tra la variabilità dei dati e la correttezza del modello utilizzato. Risulta essere una metrica maggiormente oggettiva, ma attenzione: non è una funzione di costo!
# una volta ottenuta la regressione, ne valutiamo la bontà
Y_pred = lRegr.predict(X_test)
# utilizziamo una funzione di costo di tipo "errore quadratico medio" che è del tutto simile alla funzione RSS
# con l'eccezione che il valore ottenuto viene diviso per il numero di punti in input, ottenendo quindi una media
# questo la rende un po' più "robusta" a eventuali picchi anomali, anche se è influenzato sensibilmente dal tipo di dataset
# ovviamente verrà calcolato l'errore tra i valori predetti Y_pred e i valori attesi Y_test
errore = mean_squared_error(Y_test, Y_pred)
print("Errore:", errore)
# otteniamo una misura più oggettiva utilizzando come metrica il coefficiente di determinazione
# NOTA: non è una funzione di costo, ma di punteggio, perchè può avere valori negativi e l'ottimo lo si ottiene
# avvicinandosi ad 1.0
# indicativamente, per punteggio < 0.3 il modello è inutile
# per punteggio compreso tra 0.3 e 0.5 il modello è mediocre o appena sufficiente
# per punteggio compreso tra 0.5 e 0.7 il modello è discreto
# per punteggio compreso tra 0.7 e 0.9 il modello è buono
# per punteggio > 0.9 il modello è ottimo
punteggio = r2_score(Y_test, Y_pred)
print("Score:", punteggio)
Il risultato che otteniamo sarà simile a questo (visto che i dataset vengono mischiati è normale che ad ogni esecuzione i risultati siano un po’ diversi) :
Errore: 32.74440270496865
Score: 0.5234550580862628
Il risultato non è miracoloso, ma poi capiremo anche il motivo quando andremo a disegnare su un grafico il risultato.
Intanto andiamo a leggere il valore del peso (in questo caso è unico, ma come vedete nel codice sotto, si tratta di un array), ed il bias della nostra equazione di regressione:
# visualizziamo i valori del peso e del bias trovati
print("Valore del peso:", lRegr.coef_[0])
print("Valore del bias:", lRegr.intercept_)
Valore del peso: 9.298228672473059
Valore del bias: -35.70494947431278
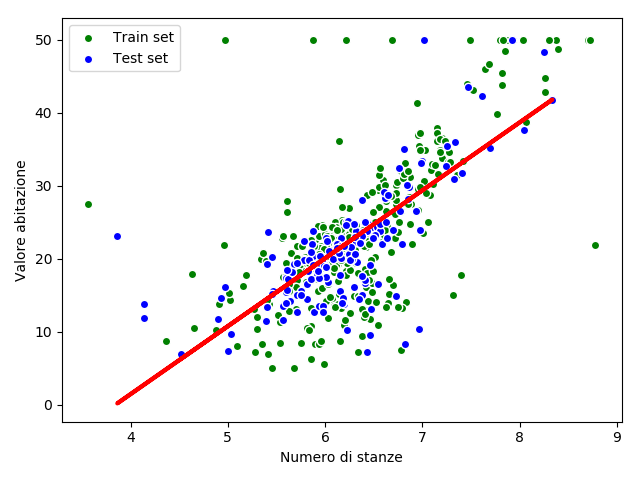
Infine andiamo a mettere su grafico il set di training (punti verdi), quello di test (punti blu) e la retta di regressione (linea rossa).
Come vedrete, il punteggio non era altissimo, ma in effetti il dataset è abbastanza diffuso a nuvola attorno alla retta di regressione, quindi di meglio non si poteva fare!
# prepariamo il grafico con i dataset di training (verdi) e di test (blue)
plt.scatter(X_train, Y_train, c="green", edgecolors="white", label="Train set")
plt.scatter(X_test, Y_test, c="blue", edgecolors="white", label="Test set")
# aggiungiamo le label degli assi e indico la posizione della legenda
plt.xlabel("Numero di stanze")
plt.ylabel("Valore abitazione")
plt.legend(loc="upper left")
# prepariamo la retta della regressione in rosso
plt.plot(X_test, Y_pred, color="red", linewidth=3)
# visualizziamo il grafico
plt.show()
See you soon!
Bene, divertitevi a sperimentare altre proprietà di questo dataset o addirittura altri dataset.
La prossima volta vedremo un esempio di regressione lineare multidimensionale che consentirà di legare la predizione a più proprietà in ingresso e quindi in definitiva ad avere un modello più robusto e realistico.
Bye!












One Comment
Pingback: La regressione polinomiale e la regolarizzazione | Maggioli Developers